Neutrinos are fundamental particles described by the standard model of particle physics as massless. One of the most important discoveries of the 20th century has been the observation of neutrino oscillations. The existence of that phenomena implies that neutrinos are massive, opening the door to physics beyond the standard model. Determining the neutrinos nature (Dirac or Majorana) and the value of their masses and hierarchy are thus major goals of modern physics. Unfortunately, those measurements are very difficult from laboratory experiments, with current bounds on the sum of the neutrino masses equal to \( \Sigma m_\nu \leqslant 6.9~{\rm eV}~(2\sigma) \).
On the other hand, neutrinos are the second most abundant particles in the Universe, only after photons, and they have large thermal velocities. The latter makes their dynamics very different to those of cold dark matter (CDM) or baryons, and is the reason why neutrinos imprint characteristic signatures on cosmological observables. At linear order, the impact of neutrino masses on quantities like the matter power spectrum is very well known and understood, and commonly used to set limits on neutrinos masses: \( \Sigma m_\nu \lesssim 0.12~{\rm eV}~(2\sigma) \). However, the information that can be extracted in this regime is limited, as the theory predictions only work on large scales. In order to detect the tiny neutrino masses, it is fundamental to use as much information as possible, as well as information from different observables.
My research is focused on studying the impact of neutrino masses on cosmological observables and searching new observables where the tiny neutrino signatures are enhanced. Together with my collaborators, we have studied the non-linear evolution of the cosmic neutrino background, extended the halo model to cosmologies with massive neutrinos and investigated the impact of neutrinos on:
- The density profile of dark matter halos [1]
- the halo mass function [1] [2]
- the halo bias [1] [2]
- galaxy properties [1]
- the BAO peak [1]
- cosmic voids [1] [2]
- the high-transmission regions of the Ly\(\alpha\)-forest [1]
- the 21cm signal in the post-reionization era [1]
- the kinetic Sunyaez-Zeldovich [1]
- redshift-space distortions [1]
Since I want to understand, characterize and parametrize the effect of neutrino masses on cosmological observables in the mildly/fully non-linear regime, I usually complement my research with numerical simulations (either N-body or hydro) with massive/massless neutrinos.
The video below, shows the spatial distribution of cold dark matter (top-right), neutrinos with masses \( \Sigma m_\nu = 0.6~{\rm eV}\) (top-left), total matter (bottom-left) and the CDM and neutrinos jointly (bottom-right) in a box of \( 100~h^{-1}{\rm Mpc}\) from one of my N-body simulations at \( z=0\). As can be seen, the neutrino density field becames fully non-linear at low-redshift, developing neutrino halos and filling up cosmic voids.
The following video shows how neutrinos cluster on small scales once their thermal velocities are low enough. The left/right panel displays the distribution of CDM/neutrinos as a function of redshift. As can be seen, at low redshifts a fraction of neutrinos have velocities low enough to cluster within dark matter halos. Notice that the density contrast in the neutrino panel is pretty low: neutrinos cluster but not much, neutrinos barely evacuate voids. This is the root of many effects induced by neutrinos on cosmological observables.
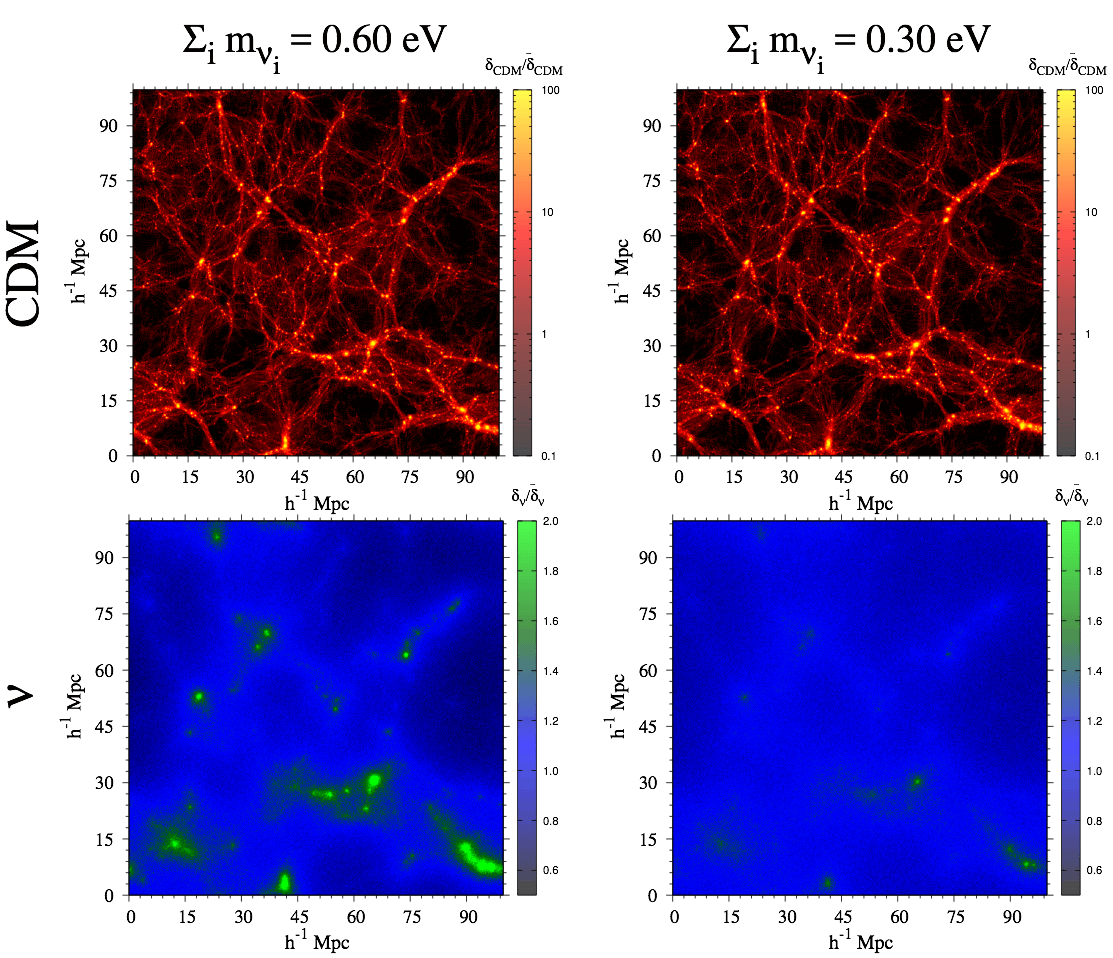
Another important effect produced by neutrinos is that they delay the growth of CDM perturbartions on small scales. The bottom image shows the distribution of CDM (top row) and neutrinos (bottom row) for a cosmology with \( \Sigma m_\nu = 0.6~{\rm eV}\) (left column) and \( \Sigma m_\nu = 0.3~{\rm eV}\) (right column) at \( z=0\). Even though the CDM distribution looks very similar among the two models, a careful look at the halos will show that those are smaller, less massive and less abundant in the model with \( \Sigma m_\nu = 0.3~{\rm eV}\) neutrinos.